Các mô hình hoặc mô hình hình học tự nhiên xuất hiện dưới dạng các hình dạng lặp lại mà đôi khi có thể được mô tả hoặc biểu diễn bằng các mô hình toán học.
Hình học trong tự nhiên và cuộc sống có nhiều dạng và hình thức, chẳng hạn như đối xứng, xoắn ốc hoặc sóng.
Lịch sử
Lần đầu tiên, các nhà khoa học và triết học Hy Lạp cổ đại - Pythagoras, Empedocles và Plato - đưa ra các câu hỏi về hình học trong tự nhiên. Bằng cách phân tích các ví dụ về các hình dạng hình học có thể dự đoán hoặc lý tưởng ở thực vật và động vật, họ đã cố gắng chứng minh trật tự và tính đối xứng trong tự nhiên.
Những nỗ lực hiện đại để nghiên cứu hình học trong tự nhiên bắt đầu vào thế kỷ 19 với nỗ lực của nhà vật lý người Bỉ Joseph Plateau, người đã phát triển khái niệm về bề mặt tối thiểu của bong bóng xà phòng. Những nỗ lực hiện đại đầu tiên tập trung vào việc chứng minh các hình dạng hình học lý tưởng và có thể dự đoán được, sau đó chuyển sang phát triển các mô hình dự đoán sự xuất hiện và biểu hiện của hình học trong tự nhiên.
Vào thế kỷ 20, nhà toán học Alan Turing đã nghiên cứu cơ chế hình thành hình thái, giải thích sự xuất hiện ở động vậtnhiều hoa văn, sọc, đốm. Một thời gian ngắn sau, nhà sinh vật học Aristide Lindenmeier cùng với nhà toán học Benoit Mandelbrot sẽ hoàn thành công trình nghiên cứu về các phân đoạn toán học lặp lại mô hình sinh trưởng của một số loài thực vật, bao gồm cả cây cối.
Khoa học
Khoa học hiện đại (toán học, vật lý và hóa học), với sự trợ giúp của công nghệ và mô hình, không chỉ cố gắng giải thích mà còn dự đoán các dạng hình học được tìm thấy trong tự nhiên.
Hình dạng và màu sắc của nhiều sinh vật sống, chẳng hạn như chim công, chim ruồi và vỏ sò, không chỉ đẹp mà còn đúng về mặt hình học, thu hút sự tò mò của các nhà khoa học. Vẻ đẹp mà chúng ta quan sát được trong tự nhiên có thể được tạo ra một cách tự nhiên, theo toán học.
Các mô hình tự nhiên quan sát được trong toán học được giải thích bằng lý thuyết hỗn loạn, hoạt động với các đường xoắn ốc và Fractal. Các mẫu như vậy tuân theo các quy luật vật lý, ngoài ra, vật lý và hóa học, sử dụng toán học trừu tượng, dự đoán hình dạng của các tinh thể, cả tự nhiên và nhân tạo.
Sinh học giải thích hình học trong tự nhiên do chọn lọc tự nhiên, trong đó các đặc điểm bình thường như sọc, đốm, màu sáng có thể được giải thích là do nhu cầu che dấu hoặc gửi tín hiệu.
Các loại hoa văn
Trong tự nhiên, có rất nhiều kiểu lặp lại xuất hiện với nhiều hình dạng hình học khác nhau. Bạn có thể tìm thấy các loại quy luật cơ bản của hình học trong tự nhiên, ảnh và mô tả của chúng bên dưới.
Đối xứng. Hình dạng hình học này là một trong những hình dạng phổ biến nhất trong tự nhiên. Phổ biến nhất ở động vậtđối xứng gương - bướm, bọ cánh cứng, hổ, cú. Nó cũng được tìm thấy trong thực vật, chẳng hạn như lá phong hoặc hoa phong lan. Ngoài ra, hình học đối xứng trong tự nhiên có thể là xuyên tâm, năm tia hoặc sáu lần, giống như những bông tuyết.

Fractals. Trong toán học, đây là những cấu tạo tự giống nhau đến vô hạn. Trong tự nhiên, không thể phát hiện ra một dạng tự lặp lại vô tận như vậy, do đó, các mẫu gần đúng của Fractal được gọi là Fractal hình học trong tự nhiên. Hình học như vậy có thể được quan sát thấy trong tự nhiên trong lá cây dương xỉ, bông cải xanh, quả dứa.
Xoắn ốc. Những dạng này đặc biệt phổ biến ở các loài nhuyễn thể và ốc. Các nhà khoa học quan sát các hình dạng xoắn ốc trong không gian, ví dụ, các thiên hà xoắn ốc. Vòng xoắn được gọi là tỷ lệ vàng của Fibonacci.

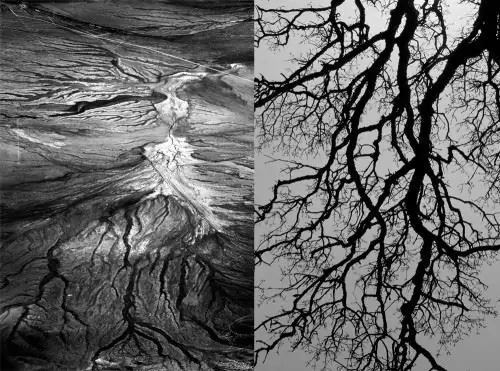
Uốn. Tính ngẫu nhiên của các hệ thống động lực học trong toán học thể hiện trong tự nhiên dưới các dạng như khúc khuỷu và dòng chảy. Hình học tự nhiên có dạng một đường đứt gãy hoặc khá cong, chẳng hạn như dòng chảy của sông.
Sóng. Chúng được gây ra bởi sự xáo trộn và chuyển động của không khí, các dòng gió, lan truyền cả trong không khí và qua nước. Trong tự nhiên, đây không chỉ là sóng biển mà còn là các đụn cát sa mạc, có thể tạo thành các hình dạng hình học - đường thẳng, đường gấp khúc và hình parabol.
Khảm. Được tạo ra bằng cách lặp lại các yếu tố giống nhau trên bề mặt. Hình học khảm trong động vật hoang dã được tìm thấy ở ong: chúng xây dựngtổ ong - tế bào lặp lại.

Hình thành các mẫu
Trong sinh học, sự hình thành màu sắc hình học là do quá trình chọn lọc tự nhiên. Trở lại giữa thế kỷ 20, Alan Turing đã tìm cách mô tả cơ chế xuất hiện các đốm và sọc trong màu sắc của động vật - ông gọi đó là mô hình khuếch tán phản ứng. Một số tế bào của cơ thể chứa các gen được kiểm soát bởi các phản ứng hóa học. Morphogen dẫn đến sự hình thành các vùng da có hắc sắc tố (đốm và sọc). Nếu hình thái có trong tất cả các tế bào da - màu của báo hoa mai sẽ có, nếu nó xuất hiện không đồng đều - là báo đốm thông thường.






