Quy tắc Titius-Bode (đôi khi được gọi đơn giản là định luật Bode) là giả thuyết cho rằng các thiên thể trong một số hệ quỹ đạo, bao gồm cả Mặt trời, quay dọc theo các bán trục tùy thuộc vào chuỗi hành tinh. Công thức cho thấy rằng, khi mở rộng ra bên ngoài, mỗi hành tinh sẽ cách xa Mặt trời gấp đôi so với hành tinh trước đó.
Giả thuyết đã tiên đoán chính xác quỹ đạo của Ceres (trong vành đai tiểu hành tinh) và sao Thiên Vương, nhưng không xác định được quỹ đạo của sao Hải Vương và cuối cùng bị thay thế bằng thuyết hình thành hệ Mặt Trời. Nó được đặt theo tên của Johann Daniel Titius và Johann Elert Bode.

Nguồn gốc
Đề cập đầu tiên về chuỗi xấp xỉ định luật Bode có thể được tìm thấy trong Các yếu tố thiên văn học của David Gregory, xuất bản năm 1715. Trong đó, ông nói: “… giả sử rằng khoảng cách từ Mặt trời đến Trái đất được chia thành mười phần bằng nhau, trong đó khoảng cách của Sao Thủy sẽ là khoảng bốn, từ Sao Kim bảy, từ Sao Hỏa mười lăm, từ Sao Mộc năm mươi hai., và từ sao Thổ chín mươi lămMột gợi ý tương tự, có lẽ được lấy cảm hứng từ Gregory, xuất hiện trong một tác phẩm do Christian Wolff xuất bản năm 1724.
Năm 1764, Charles Bonnet, trong cuốn sách Contemplation of Nature, cho biết: "Chúng tôi biết mười bảy hành tinh tạo nên hệ mặt trời của chúng ta [nghĩa là, các hành tinh chính và các vệ tinh của chúng], nhưng chúng tôi không chắc chắn rằng họ không còn nữa. " Về điều này, trong bản dịch năm 1766 của ông về tác phẩm Bonnet, Johann Daniel Titius đã thêm hai đoạn văn của chính ông ở cuối trang 7 và ở đầu trang 8. Đoạn nội suy mới không được tìm thấy trong văn bản gốc của Bonnet: cả bằng tiếng Ý. cũng không phải bản dịch tiếng Anh của tác phẩm.
Khám phá về Titius
Có hai phần trong văn bản xen kẽ của Titius. Đầu tiên giải thích chuỗi khoảng cách hành tinh từ Mặt trời. Nó cũng chứa một vài từ về khoảng cách từ Mặt trời đến Sao Mộc. Nhưng đây không phải là phần cuối của văn bản.
Điều đáng nói là đôi lời về công thức của quy tắc Titius-Bode. Hãy chú ý đến khoảng cách giữa các hành tinh và phát hiện ra rằng hầu như tất cả chúng đều cách xa nhau theo tỷ lệ tương ứng với kích thước cơ thể của chúng. Chia khoảng cách từ Mặt trời đến Sao Thổ cho 100 phần; sau đó sao Thủy cách Mặt trời bốn phần như vậy; Sao Kim - thành 4 + 3=7 phần như vậy; Trái đất - bằng 4 + 6=10; Mars - bằng 4 + 12=16.
Nhưng lưu ý rằng từ sao Hỏa đến sao Mộc có một độ lệch so với tiến trình quá chính xác này. Một không gian gồm 4 + 24=28 phần như vậy xuất phát từ sao Hỏa, nhưng cho đến nay vẫn chưa có một hành tinh nào được phát hiện ở đó. Nhưng Lord Architect có nên để nơi này trống không? Không bao giờ. Cho nênHãy giả định rằng không gian này chắc chắn thuộc về các mặt trăng chưa được khám phá của Sao Hỏa và nói thêm rằng có lẽ Sao Mộc vẫn còn một vài mặt trăng nhỏ hơn xung quanh nó mà kính thiên văn chưa nhìn thấy.

Rise of the Bode
Năm 1772, Johann Elert Bode, ở tuổi 25, đã hoàn thành ấn bản thứ hai của bản tóm tắt thiên văn Anleitung zur Kenntniss des gestirnten Himmels ("Hướng dẫn kiến thức về bầu trời đầy sao"), mà ông đã thêm chú thích sau, ban đầu không có nguồn gốc, nhưng được ghi chú trong các phiên bản sau. Trong hồi ký của Bode, người ta có thể tìm thấy tài liệu tham khảo về Titius với sự thừa nhận rõ ràng về quyền lực của anh ta.

Ý kiến Bode
Đây là cách quy tắc Titius-Bode trong phần trình bày của phần sau: nếu khoảng cách từ Mặt trời đến Sao Thổ được lấy bằng 100, thì sao Thủy sẽ cách Mặt trời bốn phần như vậy. Sao Kim - 4 + 3=7. Trái đất - 4 + 6=10. Sao Hỏa - 4 + 12=16.
Bây giờ có một lỗ hổng trong tiến trình có thứ tự này. Sau sao Hỏa, theo sau một không gian với phép tính 4 + 24=28, trong đó chưa có một hành tinh nào được nhìn thấy. Chúng ta có thể tin rằng Đấng Sáng lập của vũ trụ đã để trống không gian này không? Dĩ nhiên là không. Từ đây, chúng ta đi đến khoảng cách của Sao Mộc dưới dạng phép tính 4 + 48=52 và cuối cùng là khoảng cách của Sao Thổ - 4 + 96=100.

Hai tuyên bố này liên quan đến tất cả các kiểu cụ thể và bán kính quỹ đạo dường như có từ cổ xưathiên văn học. Nhiều giả thuyết trong số này có từ trước thế kỷ XVII.
Ảnh hưởng
Titius là học trò của triết gia người Đức Christian Freiherr von Wolff (1679-1754). Phần thứ hai của văn bản được chèn trong tác phẩm của Bonnet dựa trên tác phẩm năm 1723 của von Wolff, Vernünftige Gedanken von den Wirkungen der Natur.
Văn học thế kỷ 20 gán quyền tác giả của quy tắc Titius-Bode cho một nhà triết học người Đức. Nếu vậy, Titius có thể học hỏi từ anh ấy. Một tài liệu tham khảo cũ hơn khác được James Gregory viết vào năm 1702 trong Astronomiae Physicae etologicalae Elementa của ông, trong đó chuỗi các khoảng cách hành tinh 4, 7, 10, 16, 52 và 100 trở thành một tiến trình hình học của tỷ lệ 2.
Đây là công thức gần nhất của Newton, và cũng được tìm thấy trong các tác phẩm của Benjamin Martin và Thomas Ceard nhiều năm trước khi cuốn sách của Bonnet được xuất bản ở Đức.
Công việc xa hơn và ý nghĩa thiết thực
Titius và Bode hy vọng rằng định luật này sẽ dẫn đến việc phát hiện ra các hành tinh mới, và thực sự, việc phát hiện ra Sao Thiên Vương và Ceres, khoảng cách giữa chúng phù hợp với định luật, đã góp phần khiến giới khoa học chấp nhận nó.
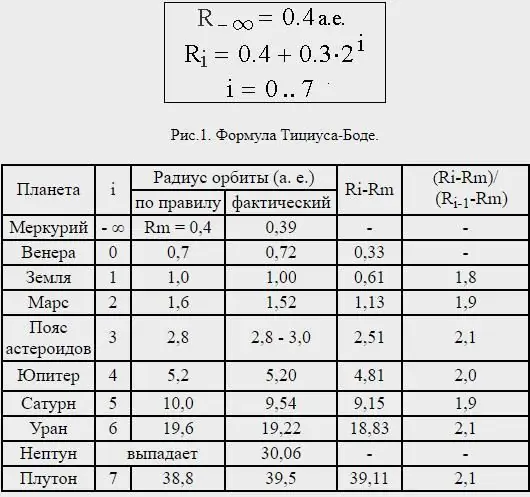
Tuy nhiên, khoảng cách của Sao Hải Vương rất không nhất quán, và trên thực tế, Sao Diêm Vương - hiện không được coi là một hành tinh - đang ở khoảng cách trung bình gần tương ứng với định luật Titius-Bode được dự đoán cho hành tinh tiếp theo bên ngoài Sao Thiên Vương.
Định luật ban đầu được công bố gần như được thỏa mãn bởi tất cả các hành tinh đã biết - sao Thủy và sao Thổ - với khoảng cách giữahành tinh thứ tư và thứ năm. Đây được coi là một con số thú vị, nhưng không có tầm quan trọng lớn, cho đến khi phát hiện ra Sao Thiên Vương vào năm 1781, phù hợp với bộ truyện.
Dựa trên khám phá này, Bode kêu gọi tìm kiếm hành tinh thứ năm. Ceres, vật thể lớn nhất trong vành đai tiểu hành tinh, được tìm thấy ở vị trí dự đoán của Bode vào năm 1801. Định luật Bode được chấp nhận rộng rãi cho đến khi Neptune được phát hiện vào năm 1846 và được cho là không phù hợp với quy luật.
Đồng thời, một số lượng lớn các tiểu hành tinh được phát hiện trong vành đai đã vượt Ceres ra khỏi danh sách các hành tinh. Định luật Bode đã được nhà thiên văn học và nhà logic học Charles Sanders Peirce thảo luận vào năm 1898 như một ví dụ về suy luận sai lầm.

Phát triển của vấn đề
Việc phát hiện ra Sao Diêm Vương vào năm 1930 càng làm vấn đề phức tạp hơn. Mặc dù nó không khớp với vị trí mà định luật Bode dự đoán, nhưng nó đúng với vị trí mà định luật dự đoán cho Sao Hải Vương. Tuy nhiên, phát hiện sau đó về vành đai Kuiper, và đặc biệt là vật thể Eris, có khối lượng lớn hơn Sao Diêm Vương nhưng không tuân theo định luật Bode, càng làm mất uy tín của công thức.
Đóng góp của Serda
Tu sĩ Dòng Tên Thomas Cerda đã tổ chức khóa học thiên văn học nổi tiếng ở Barcelona vào năm 1760 tại Chủ tịch Hoàng gia về Toán học tại Đại học Sant Jaume de Cordelle (Hoàng gia và Chủng viện Hoàng gia của Quý tộc Cordell). Trong Cerdas 'Tratado, khoảng cách hành tinh xuất hiện, thu được bằng cách áp dụng định luật thứ ba của Kepler, với độ chính xác 10-3.
Nếu chúng ta coi khoảng cách từ Trái đất là 10 vàlàm tròn đến số nguyên, cấp số nhân hình học [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, từ n=2 đến n=8, có thể được biểu thị. Và bằng cách sử dụng một chuyển động giả tưởng đều tròn đều đối với dị thường Kepler, các giá trị Rn tương ứng với tỷ lệ của mỗi hành tinh có thể thu được là rn=(Rn - R1) / (Rn-1 - R1), dẫn đến 1,82; 1, 84; 1, 86; 1,88 và 1,90, trong đó rn=2 - 0,02 (12 - n) là một quan hệ rõ ràng giữa tính liên tục Keplerian và luật Titius-Bode, được coi là một sự trùng hợp số ngẫu nhiên. Kết quả của phép tính gần bằng hai, nhưng kết quả có thể được coi là làm tròn số 1, 82.

Tốc độ trung bình của hành tinh từ n=1 đến n=8 làm giảm khoảng cách từ Mặt trời và khác với sự suy giảm đồng đều ở n=2 để phục hồi từ n=7 (cộng hưởng quỹ đạo). Điều này ảnh hưởng đến khoảng cách từ Mặt trời đến Sao Mộc. Tuy nhiên, khoảng cách giữa tất cả các đối tượng khác trong khuôn khổ của quy tắc khét tiếng mà bài báo dành cho cũng được xác định bởi động lực học toán học này.
Khía cạnh lý thuyết
Không có lời giải thích lý thuyết chắc chắn nào về quy tắc Titius-Bode, nhưng có thể là do sự kết hợp của cộng hưởng quỹ đạo và thiếu bậc tự do, bất kỳ hệ hành tinh ổn định nào cũng có xác suất lặp lại mô hình được mô tả trong lý thuyết này của hai nhà khoa học.
Bởi vì đây có thể là một sự trùng hợp toán học và không phải là "quy luật tự nhiên", nó đôi khi được gọi là một quy tắc hơn là một "định luật". Tuy nhiên, nhà vật lý thiên văn Alan Boss lập luận rằng điều này chỉ đơn giản làtrùng hợp ngẫu nhiên và tạp chí khoa học hành tinh Icarus không còn chấp nhận các bài báo cố gắng cung cấp các phiên bản cải tiến của "luật".
Cộng hưởng quỹ đạo
Cộng hưởng quỹ đạo từ các thiên thể quay quanh quỹ đạo chính tạo ra các vùng xung quanh Mặt trời không có quỹ đạo ổn định lâu dài. Kết quả mô phỏng sự hình thành hành tinh ủng hộ ý tưởng rằng một hệ hành tinh ổn định được chọn ngẫu nhiên có khả năng thỏa mãn quy tắc Titius-Bode.

Dubrulle và Graner
Dubrulle và Graner đã chỉ ra rằng các quy tắc khoảng cách theo luật lũy thừa có thể là hệ quả của các mô hình về các đám mây sụp đổ của các hệ hành tinh có hai đối xứng: bất biến quay (đám mây và nội dung của nó là không đối xứng trục) và bất biến tỷ lệ (đám mây và nội dung của nó trông giống nhau ở tất cả các tỷ lệ).
Cái sau là một đặc điểm của nhiều hiện tượng được cho là có vai trò trong việc hình thành hành tinh, chẳng hạn như nhiễu động. Khoảng cách từ Mặt trời đến các hành tinh trong hệ Mặt trời, do Titius và Bode đề xuất, đã không được sửa đổi trong khuôn khổ các nghiên cứu của Dubrulle và Graner.






