Khi đánh giá đồng cấp, ví dụ, đánh giá khả năng cạnh tranh của sản phẩm, cũng như trong bất kỳ công trình khoa học nào, cần phải thực hiện xử lý dữ liệu thống kê. Phần sau bắt đầu với việc xác định tính nhất quán của các ý kiến chuyên gia, biểu thức số của nó là hệ số hòa hợp.
Tại sao chúng ta cần đánh giá đồng thuận của chuyên gia?
Trước hết, đánh giá này là cần thiết, vì ý kiến của các chuyên gia có thể khác nhau rất nhiều về các thông số ước tính. Ban đầu, việc đánh giá được thực hiện bằng cách xếp hạng các chỉ tiêu và gán cho chúng một hệ số ý nghĩa (quyền số) nhất định. Xếp hạng không nhất quán dẫn đến các hệ số này không đáng tin cậy về mặt thống kê. Ý kiến của các chuyên gia với số lượng yêu cầu của họ (nhiều hơn 7-10) nên được phân phối theo quy luật thông thường.
Khái niệm về hệ số hòa hợp
Vì vậy. Tính nhất quán là sự phù hợp. Hệ số là đại lượng không thứ nguyên biểu thị tỷ số giữa độ phân tán và độ phân tán cực đại trong trường hợp tổng quát. Hãy khái quát những khái niệm này.
Hệ số phù hợp là một số từ 0 đến 1, thể hiện sự nhất quán của các ý kiến chuyên gia khixếp hạng một số tài sản. Giá trị này càng gần 0, tính nhất quán càng thấp. Nếu giá trị của hệ số này nhỏ hơn 0,3 thì ý kiến của các chuyên gia được cho là không thống nhất. Khi giá trị của hệ số nằm trong khoảng từ 0,3 đến 0,7, độ nhất quán được coi là trung bình. Giá trị lớn hơn 0,7 được coi là có tính nhất quán cao.
Các trường hợp sử dụng
Khi tiến hành nghiên cứu thống kê, các tình huống có thể phát sinh trong đó một đối tượng có thể được đặc trưng không phải bởi hai chuỗi, được xử lý thống kê bằng cách sử dụng hệ số hòa hợp, mà bằng một số chuỗi, được các chuyên gia có cùng cấp độ xếp hạng theo đó. tính chuyên nghiệp trong một lĩnh vực nhất định.
Phải xác định tính nhất quán của bảng xếp hạng do các chuyên gia thực hiện để xác nhận tính đúng đắn của giả thuyết mà các chuyên gia thực hiện các phép đo tương đối chính xác, điều này cho phép hình thành các nhóm khác nhau trong các nhóm chuyên gia, phần lớn được xác định bởi yếu tố con người, chủ yếu như sự khác biệt về quan điểm, khái niệm, các trường phái khoa học khác nhau, bản chất của hoạt động nghề nghiệp, v.v.
Mô tả ngắn gọn về phương pháp xếp hạng. Ưu điểm và nhược điểm của nó
Khi xếp hạng, phương pháp xếp hạng được sử dụng. Bản chất của nó nằm ở chỗ mỗi thuộc tính của đối tượng được ấn định thứ hạng cụ thể của riêng nó. Hơn nữa, mỗi chuyên gia được bao gồm trong nhóm chuyên gia, cấp bậc này được ấn địnhmột cách độc lập, dẫn đến cần phải xử lý các dữ liệu này để xác định tính nhất quán của các ý kiến chuyên gia. Quá trình này được thực hiện bằng cách tính toán hệ số hòa hợp.
Ưu điểm chính của phương pháp xếp hạng là dễ thực hiện.
Nhược điểm chính của phương pháp là:
- một số lượng nhỏ các đối tượng xếp hạng, vì khi số lượng của chúng vượt quá 15-20, rất khó để ấn định điểm xếp hạng khách quan;
- Dựa trên việc sử dụng phương pháp này, câu hỏi về mức độ quan trọng của các đối tượng được nghiên cứu vẫn còn bỏ ngỏ.
Khi sử dụng phương pháp này, phải lưu ý rằng xếp hạng dựa trên một số loại mô hình xác suất, vì vậy chúng phải được áp dụng một cách thận trọng, tùy theo phạm vi.
Hệ số xếp hạng phù hợp của Kendall
Được sử dụng để xác định mối quan hệ giữa các đặc trưng định lượng và định tính đặc trưng cho các đối tượng đồng nhất và được xếp hạng theo cùng một nguyên tắc.
Hệ số này được xác định theo công thức:
t=2S / (n (n-1)), trong đó
S - tổng chênh lệch giữa số chuỗi và số lần đảo ngược trên đối tượng địa lý thứ hai;
n - số lần quan sát.

Thuật toán tính toán:
- Các giá trị x được xếp theo thứ tự tăng dần hoặc giảm dần.
- Các giá trị y được sắp xếp theo thứ tự mà chúng tương ứng với các giá trị x.
- Đối với mỗi thứ hạng liên tiếp của y, hãy xác định có bao nhiêu giá trị xếp hạng cao hơn theo sau nó. Chúng được cộng lại và đo lường sự tương ứng của chuỗi các cấp bậc trong x và y được tính.
- Tương tự, số lượng cấp bậc của y có giá trị thấp hơn cũng được tính toán, cũng cộng lại.
- Thêm số bậc có giá trị cao hơn và số bậc có giá trị thấp hơn, dẫn đến giá trị S.
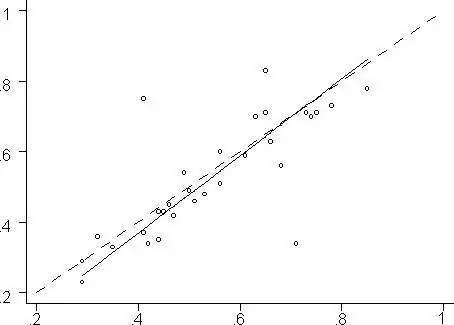
Hệ số này thể hiện mối quan hệ giữa hai biến và trong hầu hết các trường hợp được gọi là hệ số tương quan thứ hạng Kendall. Sự phụ thuộc như vậy có thể được biểu diễn bằng đồ thị.
Xác định hệ số
Nó được thực hiện như thế nào? Nếu số lượng đối tượng hoặc yếu tố được xếp hạng vượt quá 2, thì hệ số hòa hợp sẽ được sử dụng, về bản chất, là một biến thể đa dạng của mối tương quan xếp hạng.
Hãy cẩn thận. Việc tính toán hệ số hòa hợp dựa trên tỷ lệ giữa độ lệch của tổng bình phương của các bậc từ tổng bình phương trung bình của các bậc, nhân với 12, bình phương của các chuyên gia, nhân với hiệu số giữa các khối của số đối tượng và số lượng đối tượng.
Thuật toán tính toán
Để hiểu số 12 xuất phát từ đâu trong tử số của công thức tính, chúng ta hãy xem thuật toán xác định.
Đối với mỗi dòng có cấp bậc của một chuyên gia nhất định, tổng các cấp bậc sẽ được tính toán, đó là một giá trị ngẫu nhiên.
Hệ số phù hợp thường được định nghĩa là tỷ lệ của ước lượng phương sai (D) với giá trị lớn nhất của ước tính phương sai(Dmax). Hãy để chúng tôi liên tiếp xây dựng định nghĩa của những đại lượng này.
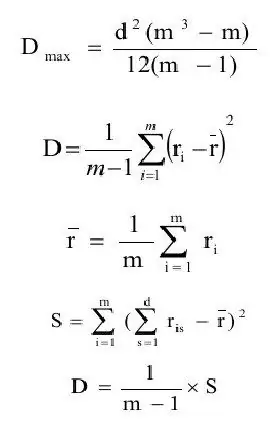
trong đó ravg- ước tính kỳ vọng;
m - số lượng đối tượng.
Thay thế các công thức kết quả liên quan đến D thành Dmaxchúng ta nhận được công thức cuối cùng cho hệ số hòa hợp:
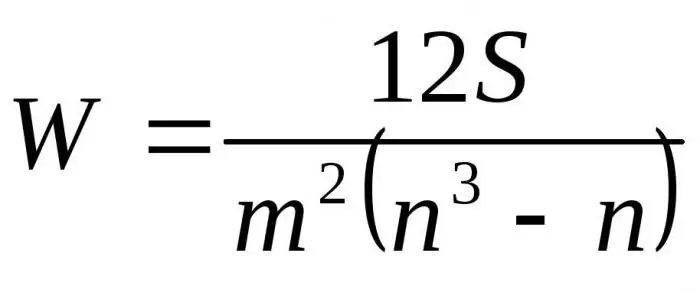
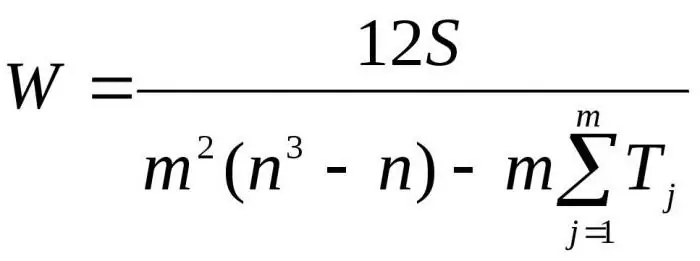
Ở đây m là số chuyên gia, n là số đối tượng.
Công thức đầu tiên được sử dụng để xác định hệ số phù hợp nếu không có cấp bậc liên quan. Công thức thứ hai được sử dụng nếu có các cấp bậc liên quan.
Như vậy, việc tính toán hệ số hòa hợp đã kết thúc. Cái gì tiếp theo? Giá trị thu được được đánh giá có ý nghĩa bằng cách sử dụng hệ số Pearson bằng cách nhân hệ số này với số chuyên gia và với số bậc tự do (m-1). Tiêu chí kết quả được so sánh với giá trị bảng và nếu giá trị của giá trị đầu tiên vượt quá giá trị cuối cùng, chúng nói lên tầm quan trọng của hệ số đang được nghiên cứu.
Trong trường hợp có các cấp bậc liên quan, việc tính toán tiêu chí Pearson trở nên phức tạp hơn một chút và được thực hiện theo tỷ lệ sau: (12S) / (d (m2+ m) - (1 / (m-1)) x (Ts1+ Ts2+ Tsn)
Ví dụ
Giả sử rằng phương pháp chuyên gia đánh giá khả năng cạnh tranh của bơ được bán trong mạng lưới bán lẻ. Hãy để chúng tôi đưa ra một ví dụ về tính toán hệ số hòa hợp. Trước khi đánh giá năng lực cạnh tranh, cần xếp hạng người tiêu dùngthuộc tính của sản phẩm này có liên quan đến việc đánh giá. Hãy giả sử rằng các đặc tính này sẽ như sau: mùi vị và mùi, tính nhất quán và hình thức, màu sắc, bao bì và nhãn mác, hàm lượng chất béo, tên thương mại, nhà sản xuất, giá cả.
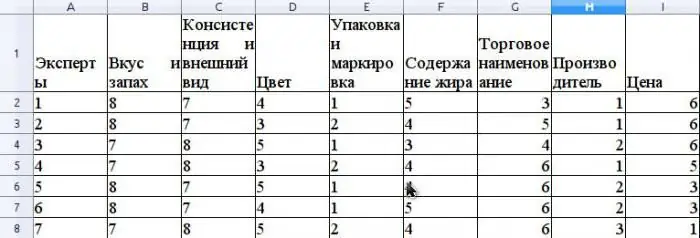
Giả sử rằng nhóm chuyên gia bao gồm 7 chuyên gia. Hình cho thấy kết quả xếp hạng các thuộc tính này.
Giá trị trung bình của r được tính là trung bình cộng và sẽ là 31,5. Để tìm S, tổng bình phương chênh lệch giữa rlàvà r trung bình, theo công thức ở trên và xác định rằng giá trị của S là 1718.
Tính hệ số hòa hợp bằng công thức mà không sử dụng các cấp bậc liên quan (các cấp bậc sẽ có liên quan nếu cùng một Cố vấn Chuyên gia có cùng cấp bậc cho các thuộc tính khác nhau).
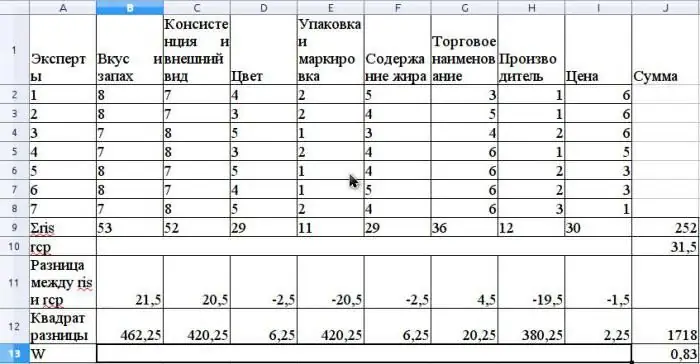
Giá trị của hệ số này sẽ là 0,83. Điều này cho thấy sự đồng thuận mạnh mẽ giữa các chuyên gia.
Kiểm tra ý nghĩa của nó bằng cách sử dụng thử nghiệm Pearson:
7 x 0,83 x (8-1)=40,7.
Bài kiểm tra dạng bảng của Pearson ở mức ý nghĩa 1% là 18,5 và ở mức 5% - 14,1.
Ví dụ thể hiện tính đơn giản và khả năng tiếp cận của phép tính đối với bất kỳ người nào biết các kiến thức cơ bản về phép tính toán học. Để giảm bớt chúng,sử dụng các biểu mẫu bảng tính.
Trong kết luận
Như vậy, hệ số hòa hợp cho thấy tính nhất quán của các ý kiến của một số chuyên gia. Càng xa 0 và càng gần 1, các ý kiến nhất quán càng nhiều. Các hệ số này phải được xác nhận bằng cách tính toán tiêu chí Pearson.






