Hàm tuyến tính là một đường thẳng được vẽ dọc theo một bề mặt. Nó có thể được chia thành nhiều loại và mô hình khác nhau. Dưới đây chúng ta sẽ xem xét các công thức để có được nó, cũng như đạt được sự hoàn hảo của nó trong mặt phẳng. Trong bản vẽ, bạn hoàn toàn có thể xác minh điều này và hiểu nó trông như thế nào.
Hàm tuyến tính y=kx + b
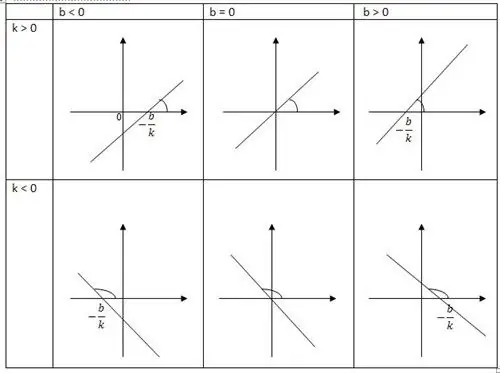
Giá trị này là thước đo chính xác của một biến trong một chế độ xem. Số tăng đề cập đến thuộc tính cơ bản của một hàm tuyến tính, nó trở nên tỷ lệ với đối số tăng dần. Nói cách khác, hàm đại diện cho một tổng quát của tỷ lệ thuận. Một đường thẳng là một đồ thị của một hàm số tuyến tính. Đây là nơi mà tên của nó đến từ. Một biến thực chạm vào một hàm thực khác.
Thuộc tính
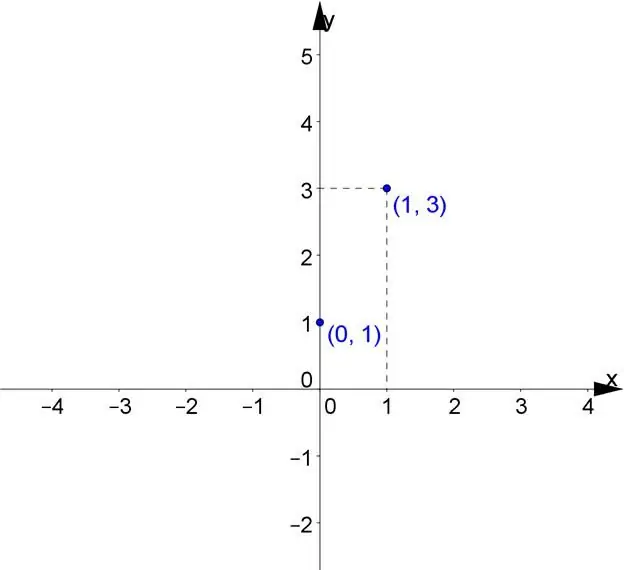
Hàm tuyến tính là một ma trận của một đường thẳng, có hướng dương của trục x. Một trong những hệ số góc xác định của nó là k, nó xác định tiếp tuyến của góc a. Đường thẳng tạo thành theo chiều dương của trục x là k. Tọa độ khác b cho biếttọa độ điểm, cũng như giao điểm của đường thẳng với trục.
Các hàm phi tuyến tính là gì?
Các hàm không tuyến tính được gọi là phi tuyến tính. Đây là một mối quan hệ toán học giữa các biến. Các giá trị phi tuyến không thể được biểu diễn dưới dạng y=ax + b. Thuật ngữ này được sử dụng trong những thời điểm cần nghiên cứu trường hợp tổng quát. Quá trình này bắt đầu với các mức độ thấp hơn. Trong trường hợp này, các hiệu chỉnh bậc hai được xem xét. Hàm như vậy có độ cong liên tục.
Phương trình phi tuyến tính được coi là tùy ý. Ví dụ về một hàm phi tuyến tính là y=x2. Thuật ngữ "hàm tuyến tính" thường được sử dụng, với sự sàng lọc và bổ sung "đồng nhất". Nó có thể được áp dụng cho một ánh xạ tuyến tính chính xác của X, là một không gian vectơ. Một hàm tuyến tính là toàn bộ hệ thống giống như nó.






