Các phát biểu về toán học như một môn khoa học trừu tượng không chỉ có trong các nguồn lịch sử, mà còn trong các điều kiện hàng ngày, nơi bạn cần thực hiện các phép tính và phép đo. Chúng tôi thực hiện các hoạt động mô tả các đối tượng về khối lượng và hình dạng mỗi ngày. Bắt đầu từ số thìa đường cho vào cà phê, tính đến mức trừ chính xác lãi suất của khoản vay.
Định nghĩa
Có thể tìm thấy những định nghĩa và phát biểu đầu tiên về toán học trong nhà triết học người Pháp Rene Descartes: “Cần phải thống nhất theo quan niệm cũ, nổi tiếng về toán học phổ thông, mọi thứ cần phải được sắp xếp theo thứ tự, hoặc đo lường các biện pháp. Và không quan trọng các phép đo được thực hiện như thế nào, con số hay âm thanh, ngôi sao hay hình vẽ.”

Ở Liên Xô, phát biểu của A. N. Kolmogorov được coi là truyền thống: “Đây là một ngành khoa học mà mối quan hệ định lượng được kết nối chặt chẽ với hình thức thực của thế giới xung quanh. Nhưng chỉ trongkhái niệm mở rộng và hoàn toàn trừu tượng.”
Nicolas Bourbaki là một nhóm các nhà khoa học Pháp đã viết một số cuốn sách về khoa học hiện đại. Nhóm được thành lập vào năm 1935, những tuyên bố về toán học nằm trong phần ngoại truyện của ấn bản đầu tiên: “Bản chất của khoa học vĩ đại này có thể được gọi là học thuyết về tác động của các vật thể lên nhau. Một số thuộc tính của các đối tượng có thể không được biết đến, nhưng chúng có thể được tính toán bằng cách sử dụng các đặc tính cơ bản, đã biết. Nó là một tập hợp các cấu trúc trừu tượng.”
Hermann Weyl nghi ngờ rằng có thể đưa ra một định nghĩa rõ ràng về toán học: “Câu hỏi về cơ sở có thể được coi là mở. Thật khó để tưởng tượng rằng theo thời gian chúng ta sẽ tìm thấy một định nghĩa toán học phù hợp với tất cả mọi người. Vì nó không phải là một môn khoa học, mà là một hoạt động sáng tạo, như âm nhạc hoặc năng lực học.”
Trích dẫn Khoa học
Những câu nói về toán học của các nhà toán học vĩ đại và những câu trích dẫn ngắn đặt ra nhiều câu hỏi hơn là trả lời chúng:
- "Đây là công cụ của bất kỳ nhà khoa học nào, giống như con dao mổ cho bác sĩ phẫu thuật" (N. Abel).
- "Chỉ có vẻ đẹp trên trái đất, cái chính ở vẻ đẹp là hình thức, hình thể lý tưởng là tỷ lệ lý tưởng, tỷ lệ bao gồm các con số. Kết luận: vẻ đẹp là những con số" (A. Augustine).
- "Lợi ích chính của toán học đối với người bình thường là nó rất khó" (A. Alexandrov).
- "Đây là khoa học của sự nghiêm khắc và rõ ràng. Về mặt đạo đức, nó có thể được coi là chân lý sáng suốt và không ưa sương mù" (L. Behrs).
- "Toán học là một cấu trúc không thể lay chuyển và là một lời tiên tri có thật" (L. Behrs).
Sai lầm và tính toán sai
Những câu nói về toán học của các nhà toán học vĩ đại nhắc nhở chúng ta rằng môn khoa học này loại trừ khả năng sai sót trong bất kỳ lĩnh vực hoạt động nào:

- "Toán học không dung thứ cho những sai lầm" (E. Bell).
- "Không có cái gọi là 'hiển nhiên'" (E. Bell).
- "Ngay cả người Hy Lạp cổ đại cũng nói" toán học ", nhưng có nghĩa là" bằng chứng "" (N. Bourbaki).
- "Năm thuật ngữ - điểm, góc, cơ thể, đường thẳng và bề mặt - đây là toán học. Nhưng quan điểm của nghệ sĩ được quyết định bởi những khái niệm này" (L. da Vinci).
- "Sai lầm của một nhà toán học có thể trả giá bằng mạng sống của không chỉ một người, mà là toàn bộ nền văn minh" (N. Bourbaki).
- "Chúng tôi lấy bột từ ngũ cốc. Nhưng cối xay nghiền những thứ họ cho vào chúng. Bạn đổ đầy hạt quinoa, bạn sẽ không nướng bánh mì. Vì vậy, đó là trong toán học, nếu bạn mắc sai lầm ngay từ đầu, bạn sẽ không nhận được kết luận đúng "(T. Huxley).
- "Không có người kém cỏi trong ngành khoa học này. Vì vậy, bạn đã đối xử với việc học một cách cẩu thả" (I. Herbart).
Cách nói về đại số
Những phát biểu về toán học của các nhà toán học vĩ đại không chỉ là một khái niệm rộng về tính toán, mà còn tập trung hẹp vào đại số, hình học và vật lý:
- "Đại số không chỉ là khoa học, đó là một cách nói về khoa học" (N. Bohr).
- "Đây không thể là công việc khó khăn, đại số được tạo ra để giải trí và giúp đỡ mọi người" (R. Bringhurst).
- "Nghệ thuật là đại số ẩn. Nó đòi hỏi tất cả thời gian vàchính cuộc sống cho những ai muốn thâm nhập bí mật của nó "(E. Bourdelle).
- "Thực hành được sinh ra từ sự kết hợp của đại số, vật lý và hình học" (R. Bacon).
- "Bạn không thể thực sự hiểu đại số nếu không trở thành một nhà thơ" (K. Weierstrass).
- "Đại số và khoa học tự nhiên cần thiết lập mối tương tác sâu sắc nhất. Nó thường được coi là một môn học bổ trợ. Nhưng cần phải xem xét những vấn đề sâu sắc hơn" (K. Weierstrass).
- "Giải quyết vấn đề trong đại số có nghĩa là chiếm được pháo đài của kẻ thù và cắm lá cờ của chính bạn lên các tháp của một thành phố bị đánh bại" (N. Vilenkin).
Hình học như lý luận trực quan
Những câu nói của những vĩ nhân về toán học và hình học có thể do chính bạn tạo ra hoặc bạn có thể tận mắt nhìn thấy sự thật.
- "Nếu bạn nhìn kỹ, mọi thứ xung quanh chúng ta đều là hình học" (A. Aleksandrov).
- "Không có mâu thuẫn, bí ẩn và rắc rối trong hình học sao?" (D. Berkeley).
- "Hình học và logic là hai điều kỳ diệu. Ở đây tất cả các định nghĩa đều rõ ràng, không ai tranh cãi các định đề, suy luận rõ ràng chuyển thành một quá trình quan sát để xác định các thuộc tính của hình và hình đó luôn ở trước mặt bạn. Tất cả những điều này tạo thành thói quen suy nghĩ tuần tự "(D. Berkeley).
- "Hình học cơ bản khiến bạn sử dụng những thủ thuật khác thường, thậm chí là dí dỏm" (E. Borel).
- "Chúng tôi mang trên vai toàn bộ gánh nặng tư tưởng khoa học Hy Lạp, chúng tôi đi theo con đường của những anh hùng thời Phục hưng, vì nền văn minh không thểtồn tại mà không có hình học "(A. Weyl).
- "Hình học mang lại trật tự cho sự hỗn loạn của mọi thứ xung quanh chúng ta" (N. Wiener).
- "Toàn bộ thế giới của chúng ta có thể được tính toán bằng hình học" (N. Wiener).
Vẻ đẹp của máy tính
Những câu nói về toán học của các nhà toán học vĩ đại khẳng định rằng vẻ đẹp của những con số và con số có thể được so sánh với nghệ thuật chân chính:

- "Con số là nhận thức đầu tiên về lý tưởng. Niềm vui là chính cảm giác rằng một số con số nhất định có thể chào đón những khoảng thời gian bằng nhau và không chấp nhận những con số mất trật tự" (A. Augustine).
- "Trực giác có thể được hợp pháp hóa trong sự nghiêm ngặt của toán học" (J. Hadamard).
- "Khoa học máy tính hình thành nên tính cách và nhân cách của con người bằng sự sáng suốt của suy nghĩ và những chân lý logic có thể được chứng minh" (A. Alexandrov).
- "Những con số, bất chấp mức độ nghiêm trọng bên ngoài, chứa đầy sức nóng bên trong của kiến thức" (A. Alexandrov).
- "Người Pitago coi toán học là khởi đầu của vạn vật" (Aristotle).
- "Khi giải quyết một vấn đề bằng việc phân tích một hành động cụ thể, có thể hình thành các kỹ thuật chung sẽ hữu ích để giải quyết những vấn đề như vậy khi chưa biết" (M. Bashmakov).
- "Khoa học đã phát triển theo cách mà tảng đá kiến thức vững chắc ngày nay có thể biến thành một mạng lưới trong một vài năm" (E. Bell).
Nghề hay cuộc sống
A. Những phát biểu của V. Voloshinov về toán học giới thiệu cho chúng ta khoa học vĩ đại. Cho phép chúng tôi coi nó như một phần củacuộc sống:
- “Toán học sẽ luôn là tình nhân của tất cả các hướng và ngành. Sự thuần khiết của toán học không có đỉnh cao, nó là vô hạn. Nó là sợi dây liên kết giữa nghệ thuật và máy tính.”
- “Chỉ có khoa học tính toán này trong quá trình phát triển của nó là không có tính trọng yếu. Tính chất này khiến cô ấy trở nên toàn năng. Ngày nay, mọi người không liên quan đến toán học đều biết rằng đây là một lực lượng lớn, sức ảnh hưởng của nó là không có giới hạn.”
- "Chỉ những người thực sự yêu khoa học mới có thể đưa ra những phát biểu đúng trong toán học."
- "Toán học đã tìm thấy một ứng dụng có ý nghĩa và có hệ thống đối với nghệ thuật trong âm nhạc, cũng như trong công việc của Pythagoras và các học trò của ông."
- "Toán học tự nó là đẹp, nhưng khi nó mang vẻ đẹp này vào sự phát triển của nền văn minh, nó trở thành một cuộc tìm kiếm sự hoàn hảo."
Những phát biểu của Pythagoras về toán học như một môn khoa học của sự khởi đầu
Câu nói nổi tiếng nhất của Pythagoras giống như một khẩu hiệu dành cho những người theo đuổi: "Mọi thứ đều là một con số."

Những câu nói khác của anh ấy, mang tính triết lý hơn, có thể hiểu theo ý bạn:
- "Làm những điều tuyệt vời, nhưng đừng hứa hẹn những điều tuyệt vời."
- "Để học các định luật toán học, trước tiên hãy cố gắng học ngôn ngữ của các con số."
- "Khám phá mọi thứ bạn thấy, hãy để tâm trí của bạn lên hàng đầu."
Những phát biểu của Lomonosov về toán học
Nhà khoa học người Nga Mikhail Vasilyevich không chỉ là một nhà khoa học vĩ đại, ông còn khám phá tất cả các ngành khoa học: từ hóa học đến thông thạo. Hầu hếtcâu nói được trích dẫn của Lomonosov về toán học như sau: “Toán học nên được biết đến bởi vì nó đặt tâm trí vào trật tự.”
Bạn cũng có thể tìm thấy các tuyên bố về các lĩnh vực cụ thể trong Lomonosov:
- "Hình học là nữ hoàng của tất cả các nghiên cứu chu đáo".
- "Hóa học là bàn tay của vật lý, và đôi mắt là chính toán học."
- "Một nhà vật lý bị mù không có khoa học tính toán".
- "Tất cả những gì còn nghi ngờ trong khoa học như đo khí dung, thủy lực và quang học, tính toán toán học sẽ làm rõ ràng, hiển nhiên và đúng sự thật."
Lập luận dí dỏm
Những câu nói về toán học của các nhà toán học vĩ đại đôi khi giống như những câu nói hóm hỉnh. Một số chỉ có thể được hiểu bởi những người hiểu biết, nhưng có những trích dẫn có sẵn cho tất cả mọi người:

- "Các đồ vật và sự vật khác nhau có thể được đặt tên giống nhau nhờ các phép tính và công thức" (A. Poincaré).
- "Một người không quen thuộc với những điều cơ bản của khoa học về các con số thì không thể thành công trong bất kỳ công việc kinh doanh nào" (R. Bacon).
- "Toán học là nghiên cứu các công thức khác nhau và mối quan hệ của chúng, chỉ là không có nội dung" (D. Hilbert).
- "Nếu không ai có thể chứng minh một định lý, họ gọi nó là tiên đề" (Euclid).
- "Toán học có thể làm được mọi thứ! Chỉ những gì cần thiết ngay bây giờ thì không thể" (A. Einstein).
Những câu nói thích hợp cho trẻ em
Chúng tôi nhớ những câu nói về toán học cho trẻ em từ những năm học, khi dưới mỗi bức chân dung của một nhà khoa học, suy nghĩ và thái độ của anh ta đối vớiKhoa học:
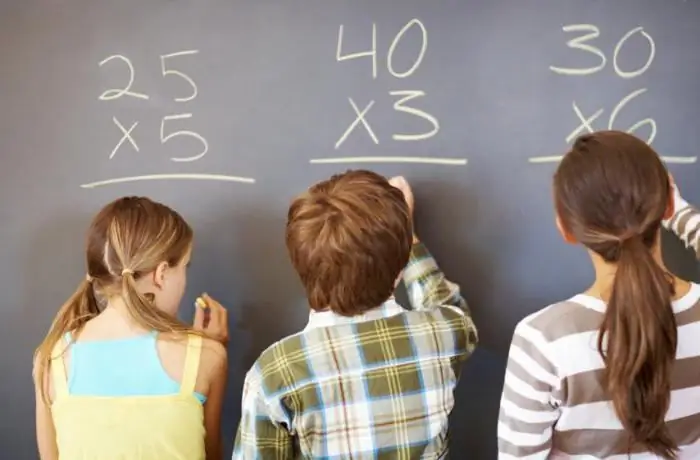
- "Trí tuệ thấu hiểu thôi chưa đủ, bạn cần phải tìm ra cách sử dụng nó" (R. Descartes).
- "Điều khó nhất là biết chính mình" (Felas).
- "Trước khi bắt đầu giải quyết một vấn đề, bạn cần đọc kỹ các điều kiện" (J. Hadamard).
Trích dẫn từ những người tuyệt vời
Phát biểu của các nhà khoa học về toán học và khoa học nói chung một lần nữa chứng minh rằng người ta đơn giản không thể làm gì nếu không có kiến thức sơ đẳng trong thế giới hiện đại:

- "Trong bất kỳ ngành khoa học nào, người ta có thể tìm thấy phần trăm sự thật chứa đựng trong khoa học tính toán" (Kant).
- "Các nhà toán học giống như người Ý. Bạn nói với họ điều gì đó, họ ngay lập tức dịch sang ngôn ngữ của họ, và chúng tôi nhận lại điều ngược lại" (Goethe).
- "Các định luật tính toán liên quan đến thế giới thực là không đáng tin cậy. Và các định luật đáng tin cậy nhất là trừu tượng" (A. Einstein).
- "Kể từ khi các nhà toán học bắt đầu tính toán thuyết tương đối, bản thân tôi cũng không hiểu nó nữa" (A. Einstein).
Những câu nói của những vĩ nhân về toán học không phải lúc nào cũng tâng bốc. Nhưng chúng ta phải thừa nhận rằng nền văn minh của chúng ta không thể tồn tại nếu không có khoa học về các con số.






