Nhiệt động lực học là một nhánh quan trọng của vật lý học. Chúng ta có thể nói một cách an toàn rằng những thành tựu của nó đã dẫn đến sự xuất hiện của kỷ nguyên công nghệ và quyết định phần lớn tiến trình lịch sử loài người trong 300 năm qua. Bài báo thảo luận về các định luật thứ nhất, thứ hai và thứ ba của nhiệt động lực học và ứng dụng của chúng trong thực tế.
Nhiệt động lực học là gì?
Trước khi xây dựng các định luật nhiệt động lực học, hãy tìm hiểu xem phần vật lý này có chức năng gì.
Từ "nhiệt động lực học" có nguồn gốc từ tiếng Hy Lạp và có nghĩa là "chuyển động do nhiệt". Có nghĩa là, ngành vật lý này tham gia vào việc nghiên cứu bất kỳ quá trình nào, do đó năng lượng nhiệt được chuyển đổi thành chuyển động cơ học và ngược lại.
Các định luật cơ bản của nhiệt động lực học được hình thành vào giữa thế kỷ 19. Khoa học về "chuyển động và nhiệt" xem xét hành vi của toàn bộ hệ thống nói chung, nghiên cứu sự thay đổi các thông số vĩ mô của nó - nhiệt độ, áp suất và thể tích, và không chú ý đến cấu trúc vi mô của nó. Hơn nữa, cái đầu tiên trong số chúng đóng một vai trò cơ bản trong việc xây dựng luật.nhiệt động lực học trong vật lý. Thật tò mò cần lưu ý rằng chúng chỉ bắt nguồn từ các quan sát thực nghiệm.
Khái niệm về hệ nhiệt động lực học

Nó có nghĩa là bất kỳ nhóm nguyên tử, phân tử hoặc các nguyên tố khác được coi là một tổng thể. Tất cả ba định luật được xây dựng cho cái gọi là hệ thống nhiệt động lực học. Ví dụ như: bầu khí quyển của Trái đất, bất kỳ sinh vật sống nào, hỗn hợp khí trong động cơ đốt trong, v.v.
Tất cả các hệ trong nhiệt động lực học đều thuộc một trong ba loại:
- Mở. Chúng trao đổi cả nhiệt và vật chất với môi trường. Ví dụ, nếu thức ăn được nấu trong nồi trên ngọn lửa mở, thì đây là một ví dụ sinh động về hệ thống mở, vì nồi nhận năng lượng từ môi trường bên ngoài (lửa), trong khi bản thân nó tỏa ra năng lượng dưới dạng nhiệt, và nước cũng bốc hơi khỏi nó (quá trình trao đổi chất).
- Đã đóng. Trong các hệ thống như vậy không có sự trao đổi vật chất với môi trường, mặc dù sự trao đổi năng lượng xảy ra. Quay trở lại trường hợp trước: nếu bạn đậy ấm bằng nắp, bạn có thể nhận được một hệ thống đóng.
- Biệt lập. Đây là một loại hệ thống nhiệt động lực học không trao đổi vật chất hoặc năng lượng với không gian xung quanh. Ví dụ là một cái phích đựng trà nóng.
Nhiệt động lực học

Khái niệm này có nghĩa là động năng của các hạt tạo thành các vật thể xung quanh, phản ánh tốc độchuyển động ngẫu nhiên của các hạt. Nó càng lớn thì nhiệt độ càng cao. Theo đó, bằng cách giảm động năng của hệ thống, chúng tôi làm mát nó.
Khái niệm này có nghĩa là động năng của các hạt tạo thành các vật thể xung quanh, phản ánh tốc độ chuyển động hỗn loạn của các hạt. Nó càng lớn thì nhiệt độ càng cao. Theo đó, bằng cách giảm động năng của hệ thống, chúng tôi làm mát nó.
Nhiệt động lực học được biểu thị bằng SI (Hệ Đơn vị Quốc tế) ở Kelvin (để vinh danh nhà khoa học người Anh William Kelvin, người đầu tiên đề xuất thang đo này). Không thể hiểu được các định luật thứ nhất, thứ hai và thứ ba của nhiệt động lực học nếu không có định nghĩa về nhiệt độ.
Sự phân chia một độ trên thang Kelvin cũng tương ứng với một độ C. Việc chuyển đổi giữa các đơn vị này được thực hiện theo công thức: TK=TC+ 273, 15, trong đó TKvà TC- nhiệt độ lần lượt tính bằng kelvins và độ C.
Điểm đặc biệt của thang đo Kelvin là nó không có giá trị âm. Số không trong đó (TC=-273, 15oC) tương ứng với trạng thái khi chuyển động nhiệt của các hạt trong hệ hoàn toàn không có, chúng dường như bị "đóng băng".
Bảo toàn năng lượng và định luật 1 nhiệt động lực học

Năm 1824, Nicolas Léonard Sadi Carnot, một kỹ sư và nhà vật lý người Pháp, đã đưa ra một đề xuất táo bạo không chỉ dẫn đến sự phát triển của vật lý mà còn trở thành một bước tiến quan trọng trong việc cải tiến công nghệ. Của anh ấycó thể được xây dựng như sau: "Năng lượng không thể được tạo ra hoặc bị phá hủy, nó chỉ có thể được chuyển từ trạng thái này sang trạng thái khác."
Trên thực tế, cụm từ của Sadi Carnot mô phỏng định luật bảo toàn năng lượng, định luật hình thành cơ sở của định luật nhiệt động lực học thứ nhất: "Bất cứ khi nào một hệ thống nhận năng lượng từ bên ngoài, nó sẽ chuyển nó thành các dạng khác, chính là là nhiệt và cơ."
Công thức toán học cho định luật thứ nhất được viết như sau:
Q=ΔU + A, ở đây Q là nhiệt lượng do môi trường truyền cho hệ, ΔU là độ thay đổi nội năng của hệ này, A là công cơ học hoàn hảo.
Quy trình Adiabatic
Một ví dụ điển hình về chúng là sự chuyển động của các khối khí dọc theo các sườn núi. Những khối lượng như vậy là rất lớn (hàng km hoặc hơn), và không khí là một chất cách nhiệt tuyệt vời. Các đặc tính được lưu ý cho phép chúng ta coi bất kỳ quá trình nào có khối khí xảy ra trong thời gian ngắn là đoạn nhiệt. Khi không khí lên dốc núi, áp suất của nó giảm xuống, nó nở ra, nghĩa là nó thực hiện công cơ học và kết quả là nó nguội đi. Ngược lại, sự chuyển động đi xuống của khối khí đi kèm với sự gia tăng áp suất trong nó, nó sẽ nén lại và do đó, nó trở nên rất nóng.
Ứng dụng của định luật nhiệt động lực học, đã được thảo luận trong tiêu đề phụ trước, được chứng minh dễ dàng nhất bằng cách sử dụng ví dụ về quy trình đoạn nhiệt.
Theo định nghĩa, do đó không có sự trao đổi năng lượng vớimôi trường, nghĩa là, trong phương trình trên, Q=0. Điều này dẫn đến biểu thức sau: ΔU=-A. Dấu trừ ở đây có nghĩa là hệ thống thực hiện công cơ học bằng cách giảm nội năng của chính nó. Cần nhắc lại rằng nội năng phụ thuộc trực tiếp vào nhiệt độ của hệ thống.
Hướng của các quá trình nhiệt
Vấn đề này liên quan đến định luật thứ 2 của nhiệt động lực học. Chắc hẳn ai cũng nhận thấy rằng nếu đưa hai vật có nhiệt độ khác nhau tiếp xúc với nhau thì vật lạnh luôn nóng lên, vật nóng nguội đi. Lưu ý rằng quá trình ngược lại có thể xảy ra trong khuôn khổ của định luật đầu tiên của nhiệt động lực học, nhưng nó không bao giờ được thực hiện trong thực tế.
Lý do cho sự không thể đảo ngược của quá trình này (và tất cả các quá trình đã biết trong Vũ trụ) là sự chuyển đổi của hệ thống sang một trạng thái có thể xảy ra hơn. Trong ví dụ được xem xét với sự tiếp xúc của hai vật thể có nhiệt độ khác nhau, trạng thái có thể xảy ra nhất sẽ là trạng thái mà tất cả các hạt của hệ sẽ có cùng động năng.
Định luật thứ hai của nhiệt động lực học có thể được xây dựng như sau: "Nhiệt không bao giờ có thể truyền một cách tự nhiên từ vật lạnh sang vật nóng." Nếu chúng ta đưa ra khái niệm entropi như một thước đo của sự rối loạn, thì nó có thể được biểu diễn như sau: "Bất kỳ quá trình nhiệt động lực học nào cũng diễn ra với sự gia tăng entropi".
Động cơ nhiệt

Thuật ngữ này được hiểu là một hệ thống mà do được cung cấp năng lượng bên ngoài nên nó có thể thực hiện công cơ học. Ngày thứ nhấtđộng cơ nhiệt là động cơ hơi nước và được phát minh vào cuối thế kỷ 17.
Định luật thứ hai của nhiệt động lực học đóng vai trò quyết định trong việc xác định hiệu quả của chúng. Sadi Carnot cũng khẳng định rằng hiệu suất tối đa của thiết bị này là: Hiệu quả=(T2- T1) / T2, ở đây T2và T1là nhiệt độ lò sưởi và tủ lạnh. Công cơ học chỉ có thể được thực hiện khi có luồng nhiệt từ vật nóng sang vật lạnh và luồng này không thể chuyển hóa 100% thành năng lượng hữu ích.
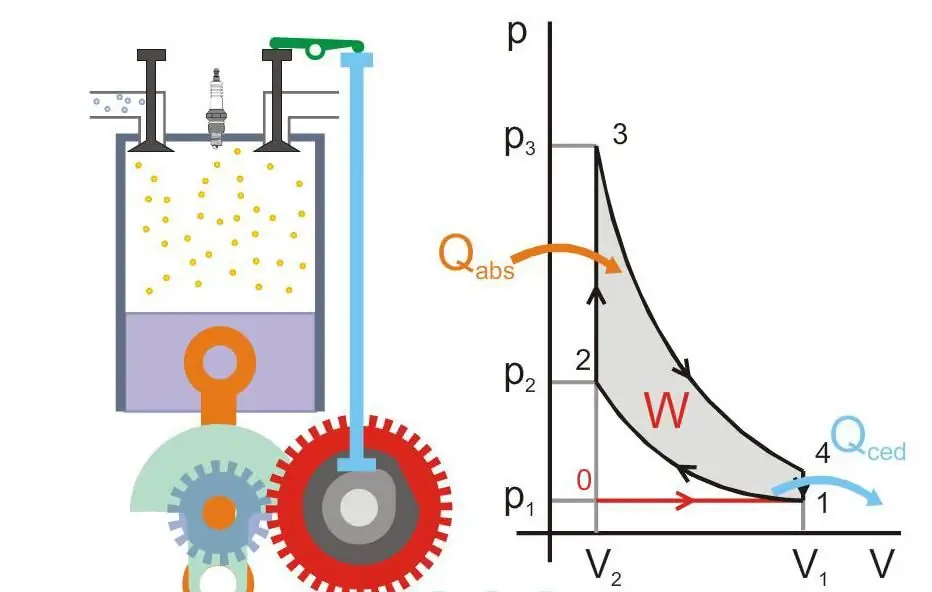
Hình bên dưới mô tả nguyên lý hoạt động của động cơ nhiệt (Qabs- nhiệt lượng truyền vào máy, Qced- tổn thất nhiệt, W - công có ích, P và V - áp suất và thể tích của khí trong piston).
Độ không tuyệt đối và định đề của Nernst
Cuối cùng, chúng ta hãy chuyển sang việc xem xét định luật thứ ba của nhiệt động lực học. Nó còn được gọi là định đề Nernst (tên của nhà vật lý người Đức, người đầu tiên đưa ra công thức này vào đầu thế kỷ 20). Định luật nói: "Không thể đạt được độ không tuyệt đối với một số lượng hữu hạn các quá trình." Có nghĩa là, không thể bằng mọi cách làm "đông cứng" hoàn toàn các phân tử và nguyên tử của một chất. Lý do cho điều này là sự trao đổi nhiệt liên tục tồn tại với môi trường.

Một kết luận hữu ích rút ra từ định luật thứ ba của nhiệt động lực học là entropi giảm khi một vật chuyển động về phía không tuyệt đối. Điều này có nghĩa là hệ thống có xu hướng tự tổ chức. Thực tế này có thểchẳng hạn như sử dụng để chuyển paramagnet sang trạng thái sắt từ khi được làm lạnh.
Điều thú vị là nhiệt độ thấp nhất đạt được cho đến nay là 5 · 10−10K (2003, phòng thí nghiệm MIT, Hoa Kỳ).






